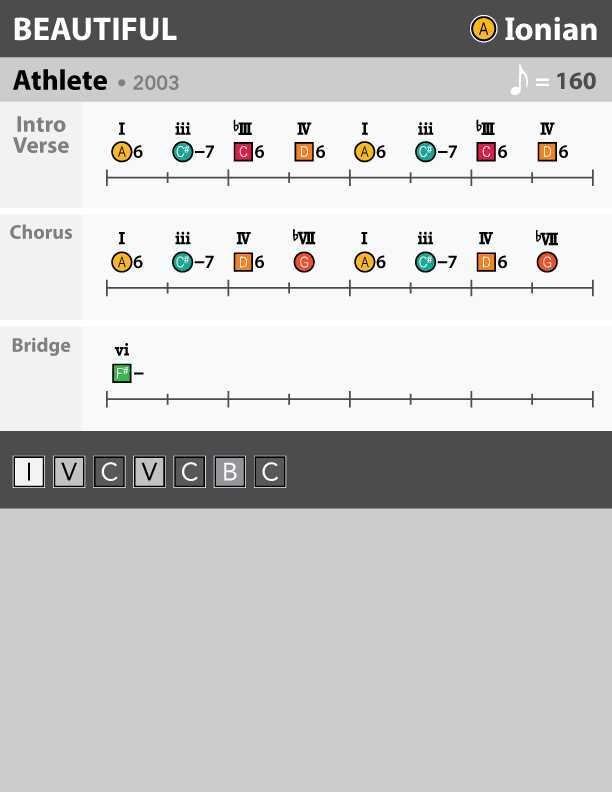
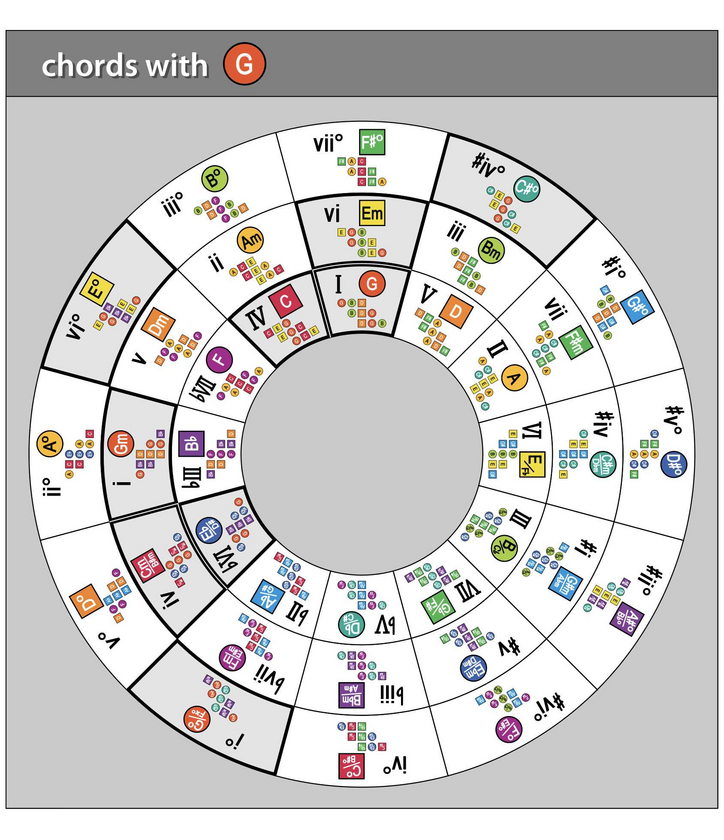
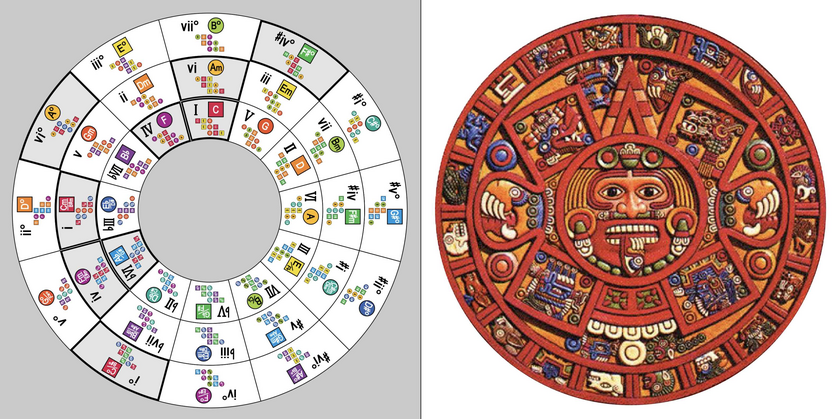
This is a "heatmap" of all chords (triads) with a G note. (The staggered stacks of notes in each cell simply illustrate the various inversions of each triad.)
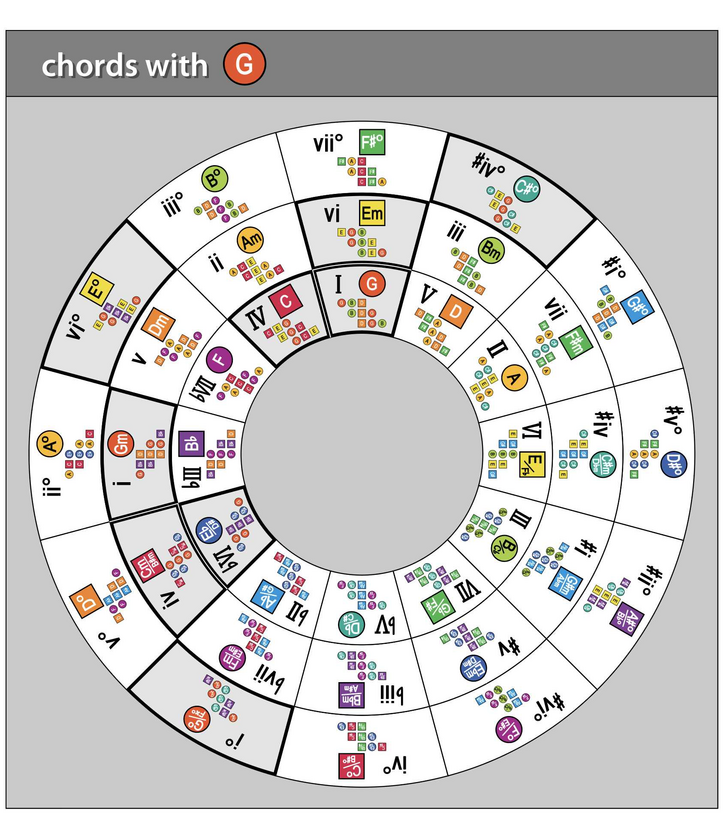
Chord progressions built from these chords tend to sound good -- due to their shared link with the G note.
You can see (and hear) what I mean as you play around with these chords.
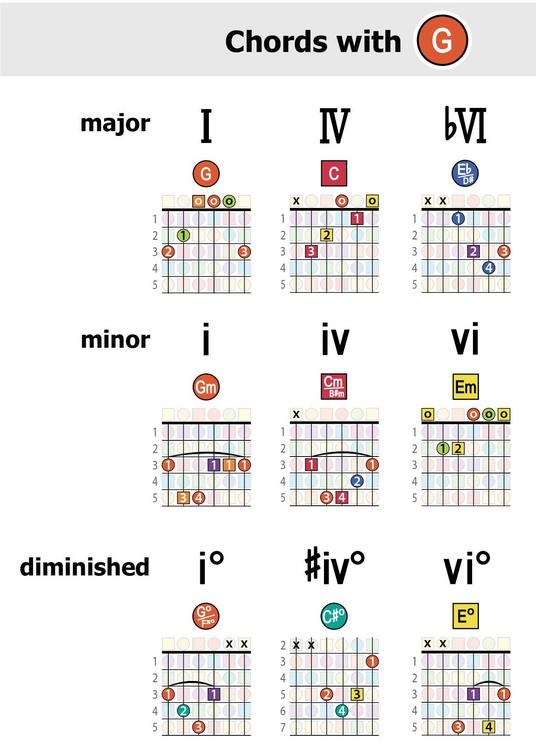
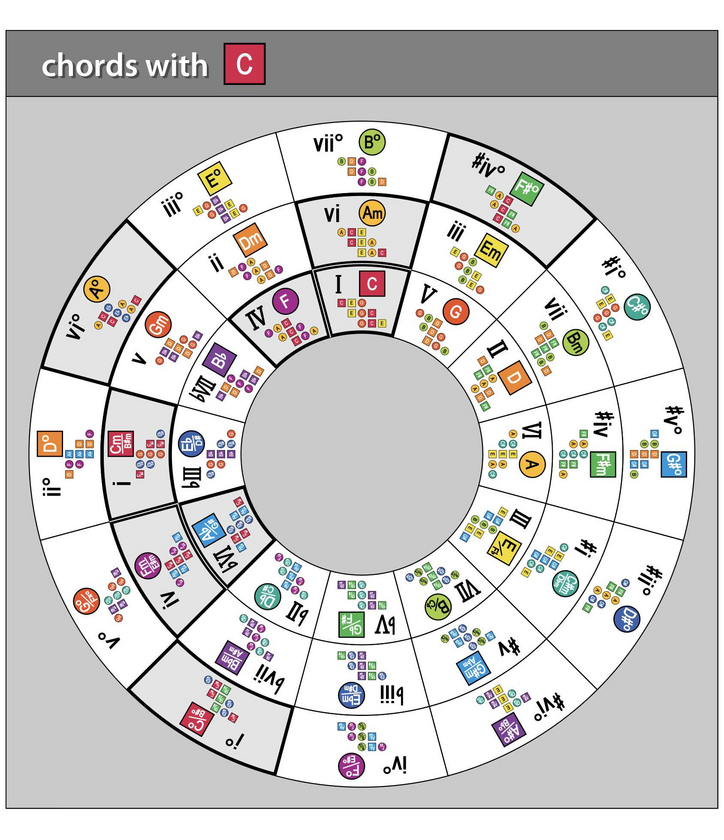
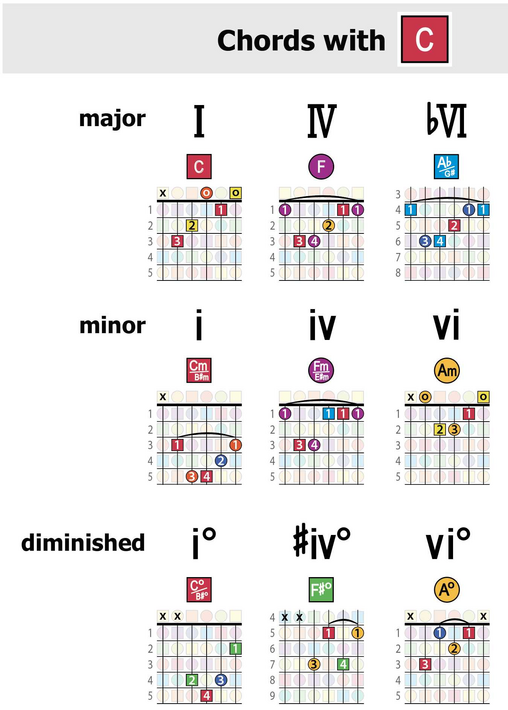
For a map of chords that include the C note, see Post #425. Notice that the harmonic positions of each chord are the same -- that is, the same numerals appear (I, IV, bVI, etc.) since the ChordMap is symmetrical across all keys.